Cofactor conditions
The Cofactor Conditions (CC) are the conditions of compatibility for the interface between the austenite and twinned martensite phases. For the type I and type II twin systems, beyond the condition that \(\lambda_2 = 1\), the CC require that one of the 2-fold axes of austenite is un-stretchable when the material undergoes phase transformation back and forth. For the compound twin system of martensite, it requires that both twinning plane normal and relative twin shear are perpendicular to the middle eigenvector of transformation stretch tensor, together with a mild inequality condition.
The mathematical forms of the Cofactor Conditions:- \(\lambda_2 =1\) where \(\lambda_2\) is the middle eigenvalue of \(\mathbf U\).
- \(\Vert\mathbf U^{-1} \mathbf e\Vert = 1\) for type I twin, \(\Vert\mathbf U \mathbf e\Vert = 1\) for type II twin, where \(\mathbf e\) is one of the 2-fold axes of austenite.
- \(\mathbf e \cdot \mathbf v_2 = 0\), \(\mathbf e^\perp \cdot \mathbf v_2 = 0\) and \((2\sqrt{1 - (\mathbf e \cdot \mathbf v_1)^2(\mathbf e \cdot \mathbf v_3)^2}+1)\det \mathbf U^2 \geq 2\) for the compound twin. The vectors \(\mathbf v_1\), \(\mathbf v_2\) and \(\mathbf v_3\) are three eigenvectors corresponding to the ordered eigenvalues of the transformation stretch tensor \(\mathbf U\).
Low-hysteresis materials
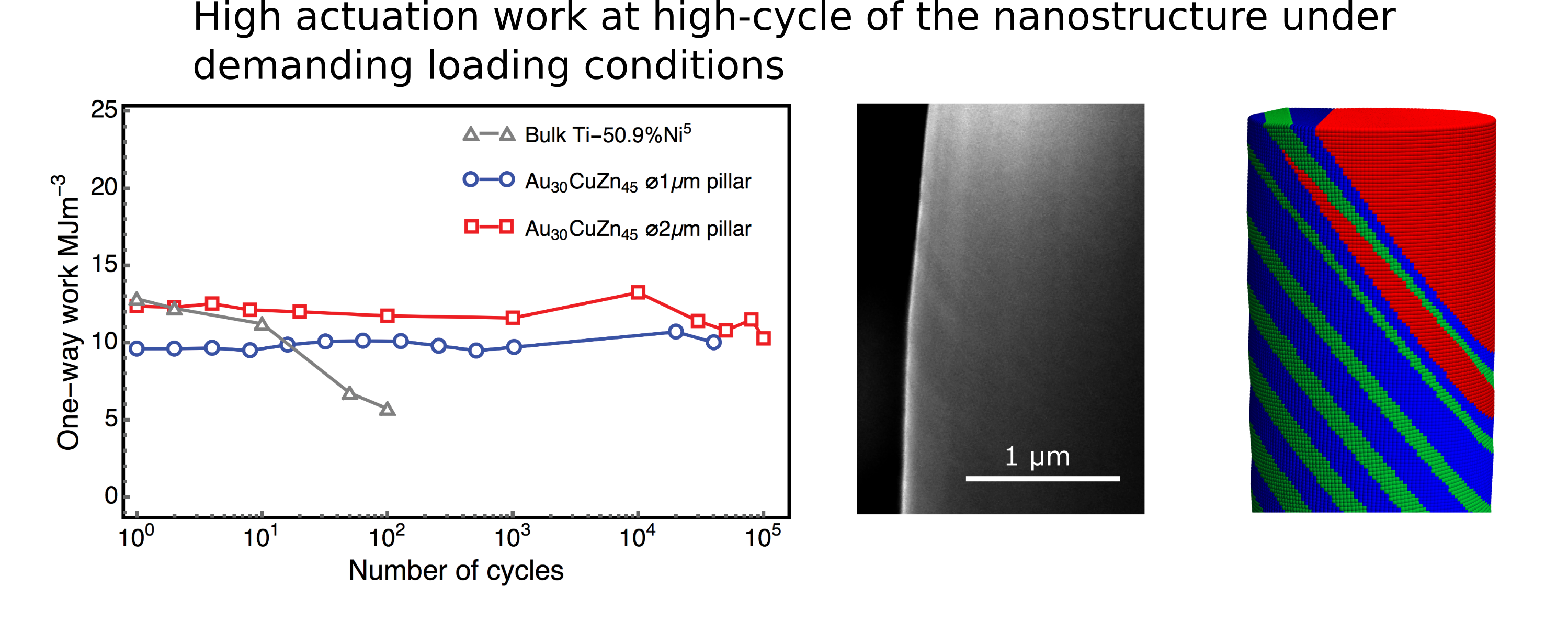
Shape memory alloys that produce and recover from large deformation driven by martensitic transformation are widely exploited in biomedical devices and microactuators. Generally they suffer from large thermal hysteresis upon transformation, and their actuation work degrades significantly within first a few cycles. In particular, such functional degradations are magnificently amplified at small scales. We demonstrate that the micropillars exhibit 12 MJ m\(^{−3}\) work and 3.5% superelastic strain even after 100,000 phase transformation cycles by making the material satisfy the compatibility conditions. Our findings confirm that the lattice compatibility dominates the mechanical behavior of phase-changing materials at nano to micron scales and points a way for smart microactuators design having the mutual benefits of high actuation work and long lifetime.
- UMN: Prof. Richard D. James
- Caltech: Prof. Kaushik Bhattacharya, Prof. Greer Julia
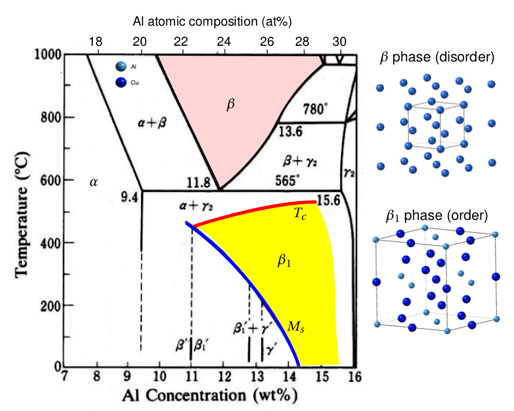
Rational materials design
We generalize the lattice metric, derived atom positions and derived symmetry of a crystal structure from phase transformation based on both theories of continuum mechanics and crystallography theory of martensite.
The mathematically derived structure from solid phase transformation underlies the rational design of complex materials. It provides a good theoretical foundation for prediction of microstructure-property relationships for transforming metals and alloys. By formalizing some crystallographic concepts -- like the 2 definitions below -- we give a heuristic of hypothesizing low-symmetry product phase structure using the high-symmetry parent phase structure.
Let the multilattice \(\mathcal M(\mathbf S, \mathcal W)\) be equal to the Bravais lattice \(\mathcal L(\mathbf E)\). An invertible matrix \(\mathbf L\in\mathbb R^{3\times3}\) is a rebase of \(\mathcal M\) if and only if there exists an integeral matrix \(\boldsymbol \Lambda \in \mathbb Z^{3\times3}\) such that \[ \mathbf L = \mathbf S^{-1}\mathbf E\boldsymbol \Lambda. \] The rebase lattice \(\mathcal M(\mathbf S', \mathcal W')\) is given by \[ \mathbf S' = \mathbf E\boldsymbol \Lambda \] and \[ \mathcal W' = \mathbf S'^{-1}(\mathcal L\cap \mathcal U(\mathbf S')) \] \[ := \{ \mathbf S'^{-1}\mathbf x: \mathbf x\in \mathcal L\cap \mathcal U(\mathbf S') \}. \]
Let the multilattice \(\mathcal M(\mathbf S, \mathcal W)\) be a multilattice that equals to some Bravais lattice. A crystal structure made of a single atomic species with \(\mathcal M\) as its underlying lattice is \[ \mathcal S(\mathcal M, \mathcal Q) = \mathcal S(\mathbf S, \mathcal W, \mathcal Q) = \mathcal M + \mathbf S\mathcal Q \] \[ := \{ \mathbf x: \mathbf x = \mathbf s + \mathbf S\mathbf q, \forall\mathbf m\in \mathcal M, \mathbf q\in\mathcal Q \}, \] where the non-empty set \[ \mathcal Q = \{ \mathbf q_\alpha \in [0, 1)^3:\alpha = 1,\cdots,\nu \}\] is the set of spatial positions occupied by atoms/molecules in the unit cell, which are usually referred as atomic positions.
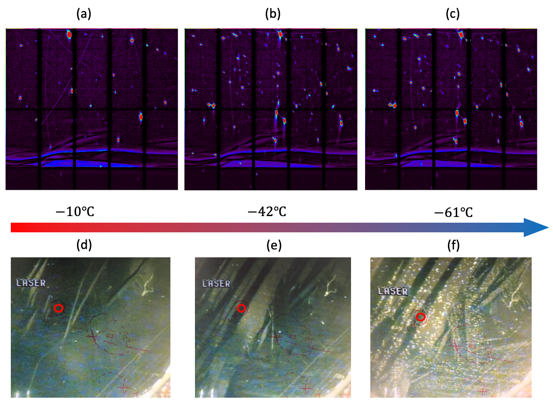
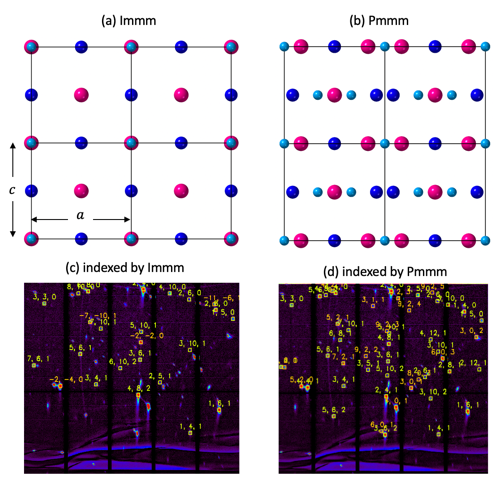
The left figure below shows X-ray Laue diffraction pattern across the phase transformation. The right one illustrates the process of finding the low-symmetry phase index by deriving an Immm structure then pertubing to Pmmm.
- ALS: Dr. Nobumichi Tamura
- CityU: Prof. Yong Yang
Nano-structured thermoelectric precipitates
For diffusional phase transformations that are almost irreversible but can be used for the synthesis of functional materials. Most of the functional composites are made by this method because the nanoscale inclusions are easily produced by the annealing process. The precipitates spread out the matrix are with the interesting applicable function. Thermoelectrics, luminescent materials, solid state fuel cells etc. are the successful applications.
Investigation of microstructures for the precipitates becomes very important because the orientations, shapes and volume fraction dominate the overall properties of the composites. All these control parameters are 3-dimensional quantities that can by visualized by the latest slice-and-view technique shown on the right. The colored chunks are precipitates seemed to be randomly distributed in whole matrix box. In fact, their orientation is predictable by a weak compatibility condition that predicts the elongated direction of the precipitates in the box lying on the crystallographically equivalent cones.